Recursively Traverse a Binary Tree

Traversal Order

A binary tree offers three primary traversal methods: Pre-order, In-order, and Post-order.

pre-order: 1->2->4->5->3->6
in-order: 4->2->5->1->3->6
post-prder: 4->5->2->6->3->1

The root node appears first in pre-order traversal and last in post-order traversal.
Leveraging this characteristic, one can uniquely construct a binary tree when provided with combinations of preorder-inorder or postorder-inorder arrays.
Note that combinations of preorder-postorder arrays aren’t sufficient for unique tree construction.

Traverse Recursively

Starting from the root node, the natural flow in a recursive traversal aligns with a pre-order traversal.

1
2
3
4
5
6
7
void traverse(TreeNode root) {
    //base case
    if(root == null) return;
    traverse(root.left); // left subtree
    traverse(root.right); // right subtree
    return;
}

The code above just traverses the binary tree without performing any additional operations. Let’s enhance this by printing the node values.

1
2
3
4
5
6
7
void traverse(TreeNode root) {
    if(root == null) return;
    System.out.println(root.val);
    traverse(root.left);
    traverse(root.right);
    return;
}

Here, during traversal, each node’s value is printed out. This is indicative of pre-order traversal where the node’s value is processed before its left and right children.

Let’s illustrate the methods to traverse and print node values using in-order and post-order approaches.

1
2
3
4
5
6
7
8
// in-order
void traverse(TreeNode root) {
    if(root == null) return;
    traverse(root.left);
    System.out.println(root.val); // handling in the mid of left and right
    traverse(root.right);
    return;
}

1
2
3
4
5
6
7
8
// post-order
void traverse(TreeNode root) {
    if(root == null) return;
    traverse(root.left);
    traverse(root.right);
    System.out.println(root.val); // handling at last
    return;
}

Backtracking

For in-order and post-order traversal, the timing of the node processing varies. The node processing occurs during the backtracking phase.

Example of postorder traversal

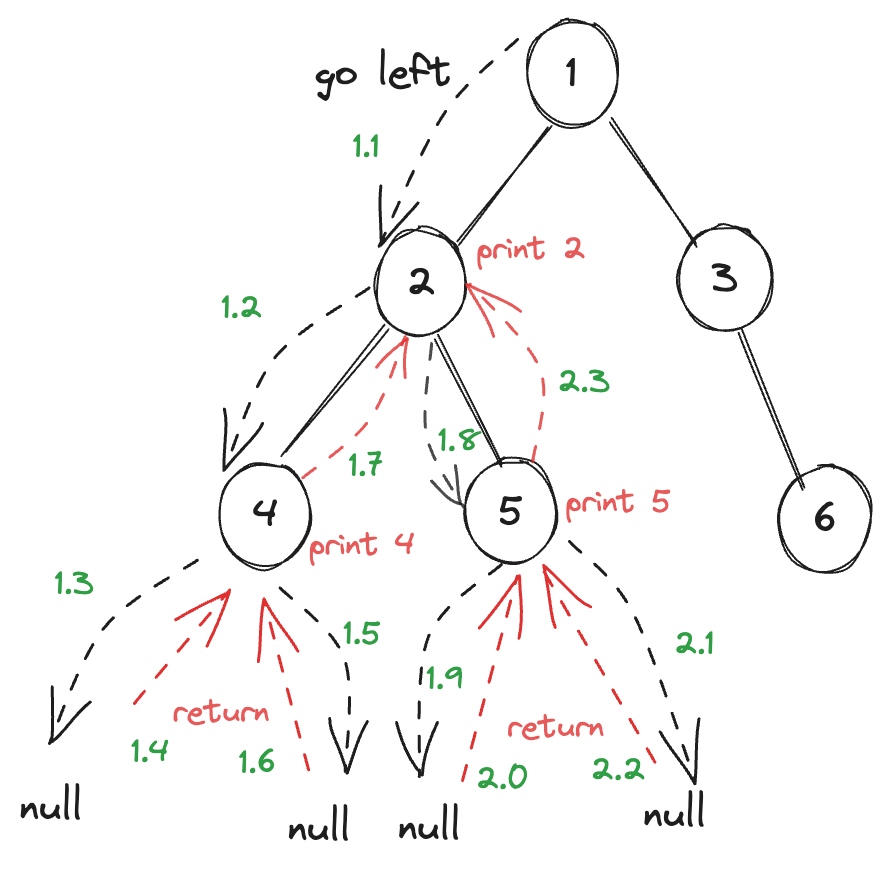
The red dotted lines represent the backtracking, and the green numbers signify the sequence of steps:

1.1-1.3: Traverse left until the leftmost leaf node (value 4).
1.4-1.6: Leaf node’s left and right children are null, so return to the leaf node and print the value 4.
1.7: Return to node 2.
1.8: Traverse to the right child node (value 5).
1.9-2.2: As both the left and right children of the leaf node are null, return to the leaf node and print the value 5.
2.3: Return to node 2 and print its value, resulting in the post-order output 4->5->2 for the left subtree.

This is just a segment of the recursive process, providing my understanding into the mechanics of tree traversal when gruelingly grinding on LeetCode.

Contents

Traversal Order

Traverse Recursively

Backtracking